
Add the two equations together to eliminate the y, then solve for x.Īny of the other methods can be used to check your answer, or you can plug in the x and y values to insure that both equations give you true statements. The system of equations are solved by eliminating a variable and solving for the remaining variable. The Elimination Method : Both equations are in standard form: A x + B y = C. Solve for a in the second equation, then substitute the second equation into the first. The systems are solved by solving for one variable in one of the equations, then substituting that equation into the second equation. Type 2: One variable can be easily isolated. The system is solved by substituting the equation with the isolated term into the other equation: Type 1: One variable is by itself or isolated in one of the equations. The Substitution Method: There are two different types of systems of equations where substitution is the easiest method. The intersection of the two lines will represent the solution to the system of equations. In this case, the calculator can be used to graph both equations. It may be easier to graph the equations by converting the standard form of each equation to slope-intercept form. The Graphing Method: When there is one variable solved in both equations, it is easy to use a graphing calculator. Solving systems of equations by graphing is done by graphing each equation in the system and identifying the point (s) of intersection. They are listed and described briefly below.


There are essentially three different methods to solve systems of equations algebraically. How can a system of equations be solved by elimination? How can a system of equations be solved by substitution? How can a system of equations be solved by graphing? Given verbal and/or algebraic descriptions of situations involving systems of two variable linear equations, the student will solve the system of equations. The student is expected to:Ī(5)(C) solve systems of two linear equations with two variables for mathematical and real-world problems The student applies the mathematical process standards to solve, with and without technology, linear equations and evaluate the reasonableness of their solutions. The student is expected to:Ī(3)(F) graph systems of two linear equations in two variables on the coordinate plane and determine the solutions if they existĪ(3)(G) estimate graphically the solutions to systems of two linear equations with two variables in real-world problemsĪ(5) Linear functions, equations, and inequalities.
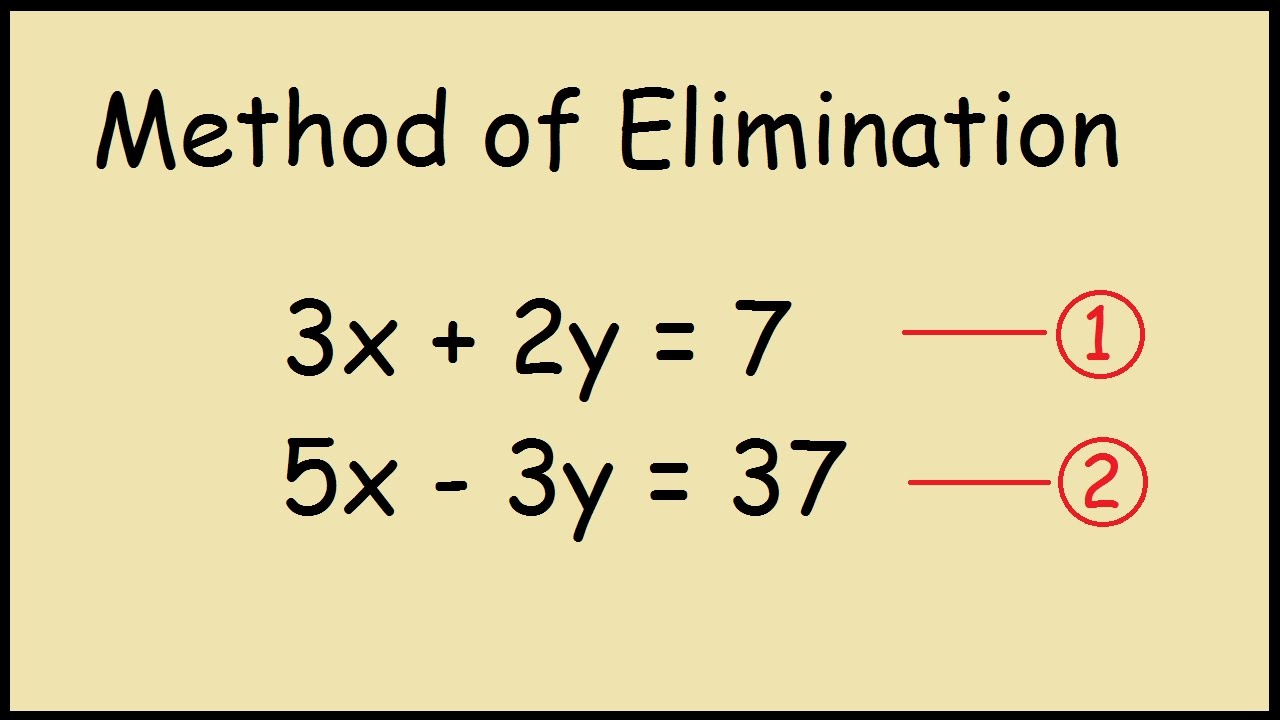
The student applies the mathematical process standards when using graphs of linear functions, key features, and related transformations to represent in multiple ways and solve, with and without technology, equations, inequalities, and systems of equations. We're going to learn to use a variety of methods to solve a system of equations.Ī(3) Linear functions, equations, and inequalities.


 0 kommentar(er)
0 kommentar(er)
